
We use the fact (Exercise 77 in Section 10.3) that the graph of r f( ) is the graph of r f() rotated counterclockwise about the origin through an angle. The neighborhood of (-1,0) and (0,1) to lie on the line y=x+1. much more convenient to use polar equations than Cartesian equations. When we plot points in Cartesian coordinates, we start at the origin and move a distance right or left given by the (x)-coordinate of the point, then move up or down according to the (y)-coordinate. Points(-1,0) and (0,1) as well as near θ =π/4 and θ =5π/4 shown to beĬonsistent with the line y=x+1, what about the remaining points near theĪnything intuitive about the graph of d( θ) nor the graphs of r= sin θĪnd r= cos θ that would insist on the points in Section 10.2 Polar Graphs Subsection Graphing in Polar Coordinates. Note the θ =π/4 and θ =5π/4Ĭorresponds to the line y=x+1, so that r→±∞ at these values of θ explains the linear Also, as θ approaches π/4 from the left, r → It may be useful to graphs d( θ) to visualize the problem.įrom looking at this graph of d( θ), it is clear that when θ=0, r=1/d=-1. Let the value of the denominator be d=sin θ – cos θ. Point is the development, we can observe a few points. This explains the Cartesian points (-1,0) and (0,1). It is clear that at θ=0, sinθ=0 and cosθ=1. Plot these again from 0 to π/4 to get a sense of what Understanding of each of the denominator terms, sinθ and cosθ.
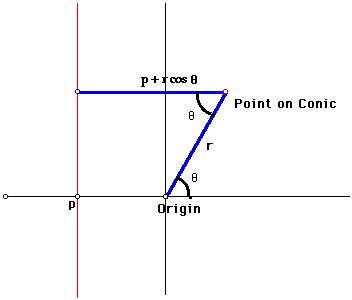
To begin this study, a natural starting point may be an
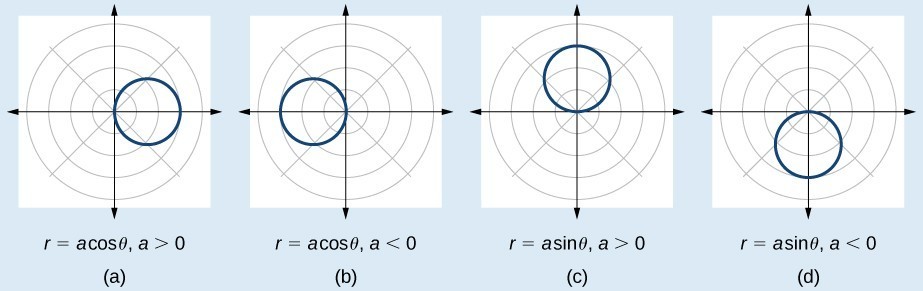

Many explorations in polar coordinates, we come to expect a symmetry orĭoes this graph have the appearance of a straight line y=x+1 (in Cartesian For example, you can reflect an object over the x-axis and then the y-axis.
POLAR EQUATION OF A LINE THROUGH THE ORIGIN GRAPHING SERIES
Note that we can use more than one line in a series of reflections. The graph of the equation in polar coordinates: Any line can be a line of reflection, but the axes and the line through the origin with slope 1 are most common.


 0 kommentar(er)
0 kommentar(er)
